퍼셉트론은 프랑크 로젠블라트(Frank Rosenblatt)가 고안한 인공 신경망으로 실제 뇌의 뉴런과 비슷하게 동작합니다.
퍼셉트론 모델은 여러 입력값을 받아 가중치를 곱한 뒤 합하여 활성함수에 넣어 결과를 얻어냅니다.

이 간단한 단층 퍼셉트론을 이용하여 비트연산을 학습시켜 보겠습니다.
학습시키기 전에 학습시킬 데이터를 생성해야 하기 때문에 데이터를 생성해주는 함수를 만들겠습니다.
def generate_or_data():
x = np.random.randint(0, 2, size=(100, 2))
y = np.array([x[:, 0] | x[:, 1]]).T
return x, y
def generate_and_data():
x = np.random.randint(0, 2, size=(100, 2))
y = np.array([x[:, 0] & x[:, 1]]).T
return x, y
def generate_xor_data():
x = np.random.randint(0, 2, size=(100, 2))
y = np.array([x[:, 0] ^ x[:, 1]]).T
return x, y
def plot_data(x, y):
plt.scatter(x[:, 0], x[:, 1], c=y[:, 0], cmap=plt.cm.bwr)
plt.show()
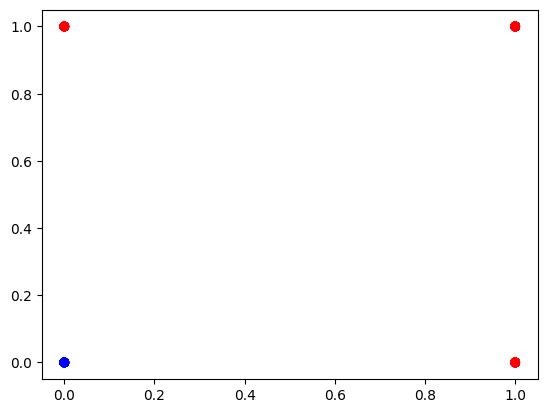
plot_data(*generate_or_data())
plot_data(*generate_and_data())
plot_data(*generate_xor_data())OR
class Model(tf.Module):
def __init__(self):
self.w = tf.Variable(tf.random.uniform(shape=[2, 1], minval=-1, maxval=1))
self.b = tf.Variable(tf.random.uniform(shape=[1], minval=-1, maxval=1))
def __call__(self, x):
y = tf.sigmoid(tf.matmul(x, self.w) + self.b)
return y
def loss_fn(x, y):
return tf.reduce_mean(tf.square(model(x) - y))학습시킬 모델과 손실함수를 정의 해 주겠습니다.
비트연산자는 두개의 입력을 받아 하나의 출력을 내보내기 때문에
가중치는 (2, 1) 형태의 배열이 필요합니다.
model = Model()
def train(x, y, lr=0.1):
with tf.GradientTape() as tape:
loss = loss_fn(x, y)
grads = tape.gradient(loss, [model.w, model.b])
model.w.assign_sub(lr * grads[0])
model.b.assign_sub(lr * grads[1])
def predict(x):
return model(x)
def accuracy(x, y):
return tf.reduce_mean(tf.cast(tf.equal(tf.round(predict(x)), y), tf.float32))모델을 생성하고, 학습을 시켜줄 경사하강법 알고리즘으로 작성된 함수를 만들어 줍니다.
그 뒤 모델의 정확도를 구하기 위하여 정확도를 계산해주는 함수를 만들어 줍니다.
x, y = generate_or_data()
x = tf.constant(x, dtype=tf.float32)
y = tf.constant(y, dtype=tf.float32)
plot_data(x, y)
for i in range(1000):
train(x, y)
if i % 100 == 0:
print('loss: {:.4f}, accuracy: {:.4f}'.format(loss_fn(x, y), accuracy(x, y)))데이터를 생성하고 학습시키면 정확도가 1이 나올정도로 정확하게 학습됐다는건 알 수 있게 됐습니다.
어떤 방식으로 값을 판단하는지 알아보기 위해 출력되는 값의 정도를 투명도로 정해서 어떻게 나오는지 보겠습니다.
def plot_decision_boundary():
x = np.linspace(0, 1, 100)
y = np.linspace(0, 1, 100)
x = tf.constant(x, dtype=tf.float32)
y = tf.constant(y, dtype=tf.float32)
xx, yy = np.meshgrid(x, y)
z = predict(np.c_[xx.ravel(), yy.ravel()])
z = z.numpy().reshape(xx.shape)
plt.contourf(xx, yy, z, cmap=plt.cm.bwr, alpha=0.2)
plt.show()
plot_decision_boundary()
AND
or 코드를 가져다 사용하겠습니다.
model = Model()
x, y = generate_and_data()
x = tf.constant(x, dtype=tf.float32)
y = tf.constant(y, dtype=tf.float32)
plot_data(x, y)
for i in range(1000):
train(x, y)
if i % 100 == 0:
print('loss: {:.4f}, accuracy: {:.4f}'.format(loss_fn(x, y), accuracy(x, y)))
plot_decision_boundary()변한건 데이터를 생성해주는게 or에서 and로 변한 것 밖에 없습니다.
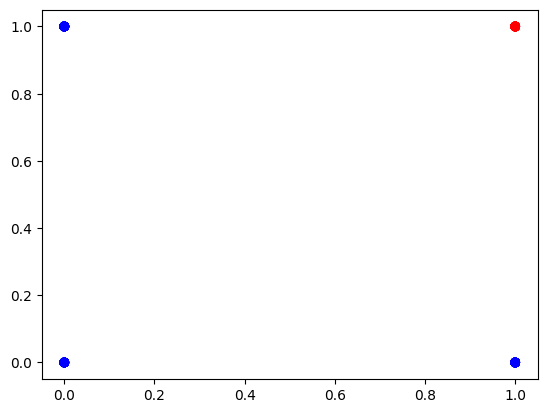
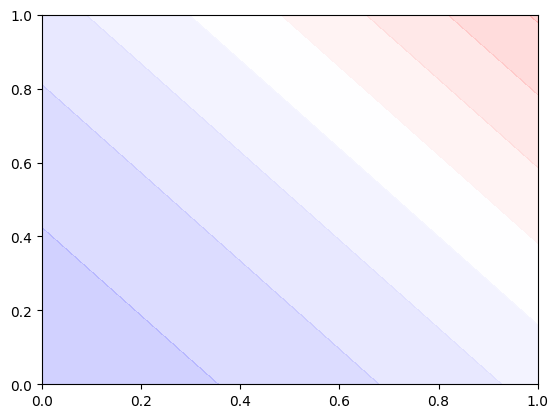
학습시켜보면 아까전 or과 다르게 (0, 1), (1, 0) 일때가 빨간색에서 파란색으로 변했습니다.
이걸로 AND도 학습이 제대로 되었다는걸 볼 수 있습니다.
XOR
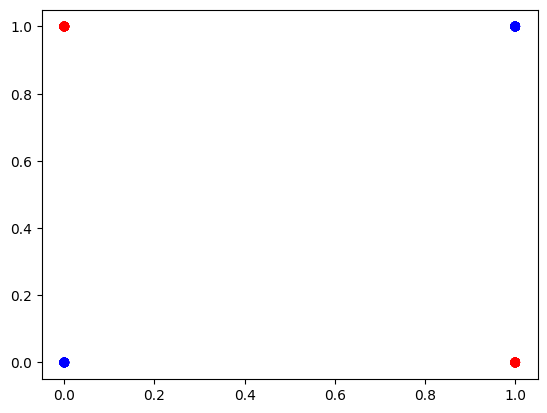
model = Model()
x, y = generate_xor_data()
x = tf.constant(x, dtype=tf.float32)
y = tf.constant(y, dtype=tf.float32)
plot_data(x, y)
for i in range(10000):
train(x, y)
if i % 100 == 0:
print('loss: {:.4f}, accuracy: {:.4f}'.format(loss_fn(x, y), accuracy(x, y)))
plot_decision_boundary()데이터를 xor로 바꿔서 학습시켜 보겠습니다. 학습도 10배 더 늘렸습니다.
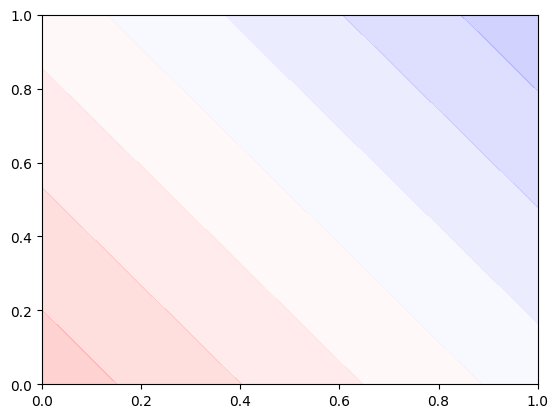
이번엔 정확도도 0.8로 나오고 판정 기준도 뭔가 이상한걸 볼 수 있습니다.
단층 퍼셉트론으로는 XOR 문제를 해결할 수 없기 때문입니다.
단층 퍼셉트론은 최고차항이 1로 일차 함수인데 일차 함수로는 아무리 선을 잘 그어봐도 XOR을 판정을 내릴 수 없습니다.
다층 퍼셉트론을 이용해서 XOR 문제를 풀어보겠습니다.
class Layer(tf.Module):
def __init__(self, out_dim, weight_init=tf.random.uniform, activation=tf.identity):
self.out_dim = out_dim
self.weight_init = weight_init
self.activation = activation
self.w = None
self.b = None
@tf.function
def __call__(self, x):
self.in_dim = x.shape[1]
if self.w is None:
self.w = tf.Variable(self.weight_init(shape=[self.in_dim, self.out_dim]))
if self.b is None:
self.b = tf.Variable(tf.zeros(shape=[self.out_dim]))
z = tf.add(tf.matmul(x, self.w), self.b)
return self.activation(z)
class MLP(tf.Module):
def __init__(self, layers):
self.layers = layers
@tf.function
def __call__(self, x, preds=False):
for layer in self.layers:
x = layer(x)
return x
model = MLP([
Layer(2, activation=tf.sigmoid),
Layer(1, activation=tf.sigmoid)
])
x, y = generate_xor_data()
x = tf.constant(x, dtype=tf.float32)
y = tf.constant(y, dtype=tf.float32)
plot_data(x, y)
def accuracy(x, y):
return tf.reduce_mean(tf.cast(tf.equal(tf.round(model(x)), y), tf.float32))
def loss_fn(x, y):
return tf.reduce_mean(tf.square(model(x) - y))
def train(x, y, lr=0.1):
with tf.GradientTape() as tape:
loss = loss_fn(x, y)
optimizer = tf.keras.optimizers.Adam(learning_rate=lr)
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
def plot_decision_boundary():
x = np.linspace(0, 1, 100)
y = np.linspace(0, 1, 100)
x = tf.constant(x, dtype=tf.float32)
y = tf.constant(y, dtype=tf.float32)
xx, yy = np.meshgrid(x, y)
z = model(np.c_[xx.ravel(), yy.ravel()])
z = z.numpy().reshape(xx.shape)
print(z)
plt.contourf(xx, yy, z, cmap=plt.cm.bwr, alpha=0.2)
plt.show()
for i in range(1000):
train(x, y)
if i % 100 == 0:
print('loss: {:.4f}, accuracy: {:.4f}'.format(loss_fn(x, y), accuracy(x, y)))
plot_decision_boundary()Gradient Descent를 사용하면 학습이 잘 되지 않아 Adam Optimizer를 사용했습니다.
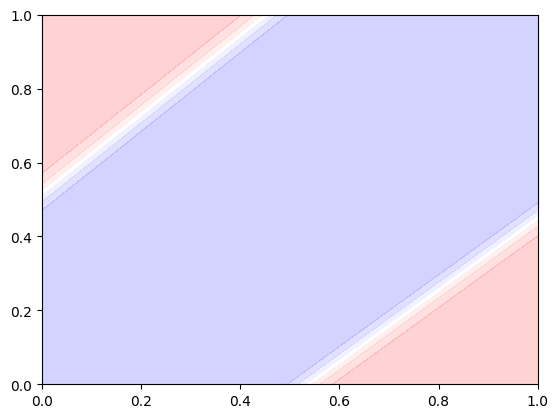
아주 아름답게 학습되서 양쪽 끝만 빨간색인걸 볼 수 있습니다.
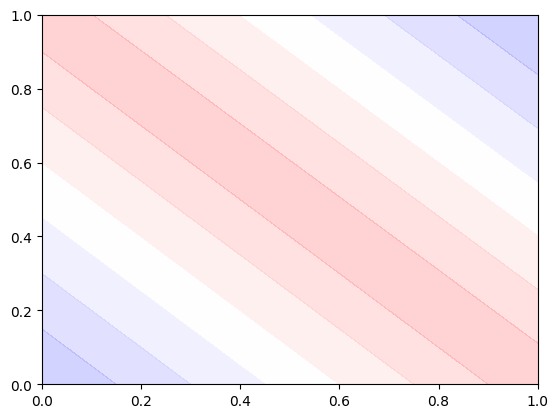
이러한 것도 볼 수 있습니다.
'인공지능' 카테고리의 다른 글
| 선형 회귀(Linear Regression) (1) | 2022.10.28 |
|---|